Mathematicians Solve The Topological Mystery Behind The “Brazuca” World Cup Football Just in time for the World Cup final

The 1970 World Cup in Mexico is famous in footballing terms because of its attacking style of play and because it was won by a talented Brazilian team featuring Pelé, the player widely regarded as the best in history.

But this World Cup was also significant for topological reasons. It was the first to feature a ball with icosahedral symmetry — the famous Adidas Telstar, which the company made by stitching together 12 black pentagonal panels and 20 white hexagonal panels.

That’s important for topologists because icosahedral symmetry is one of only three Platonic symmetry groups, the other two being tetrahedral and octahedral symmetry groups.

What’s interesting about this ball is that it has a molecular analogue in the form of the fullerene C60—the famous football-shaped molecule which was discovered later in 1985. This too is made up of pentagonal and hexagonal carbon rings that together take on the exact shape of the Telstar.

Adidas continued to use balls with icosahedral throughout the 1970s, 80s and 90s until the 2006 World Cup in Germany when it introduced a ball with tetrahedral symmetry, known as the Teamgeist. Unlike previous balls, this one was made using 14 curved panels that together made it topologically equivalent to a truncated octahedron.

Just like the Telstar, the Teamgeist has a molecular analogue too in the form of fullerenes that obey tetrahedral symmetry.

But what of the third and final Platonic symmetry group involving octahedral symmetry? It turns out that Adidas has addressed this shortcoming with its current World Cup ball: the Brazuca now being used in Brazil.

The Adidas Brazuca is made from six panels each with a four-leaf clover shape that knit together like a jigsaw to form a sphere. This ball turns out to have octahedral symmetry, finally completing all of the Platonic symmetry groups.

But here’s the thing: nobody knows whether the Adidas Brazuca has a molecular analogue in the form of a fullerene with octahedral symmetry. Certainly nobody has ever seen a fullerene with this kind of symmetry. Indeed, topologists have never worked out whether it is even possible for a fullerene to form this shape given that it must be constructed from pentagons and hexagons in such a way that no two pentagons touch.

At least until now. Today, Yuan-Jia Fan and Bih-Yaw Jin at the National Taiwan University in Taipei announce the happy news that fullerenes can indeed form ball-shaped molecules with octahedral symmetry, just like the Adidas Brazuca.

Their method is relatively straightforward. They start with a flat sheet of graphene made from hexagonal rings of carbon. From this, they cut a template shape, such as a triangle, that they then glue together to form various ball-shaped molecules.

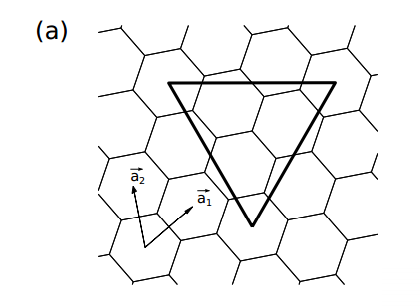
To keep track of the symmetry, their approach is to paste the template shapes onto the faces of polyhedra with known symmetry. The adjacent carbon hexagons then knit together to form a polygon with the same symmetry. However, where the vertices of the triangles meet, shapes other than hexagons can form too, such as pentagons.

An important part of this problem is that pentagons cannot be adjacent in fullerenes so anything that forms this kind of structure is ruled out.

So for example, Yuan-Jia and Bih-Yaw construct a fullerene with icosahedral symmetry by cutting 20 equilateral triangles out of graphene and then pasting them onto the triangular faces of an icosahedron. This creates a shape made of 20 hexagons with 12 pentagons at the vertices of the icosahedron. In other words, this cut-and-paste procedure produces C60, the molecular analogue of the Telstar.

The trick for creating a fullerene with octahedral symmetry is to start with a polyhedron that already has this symmetry, such as a cube with the corners cut off and the edges bevelled, known as a cantellated cube.

The next question is what template shape should they paste onto this cube. Yuan-Jia and Bih-Yaw try several showing that a remarkable variety of shapes with octahedral symmetry can be formed in this way.

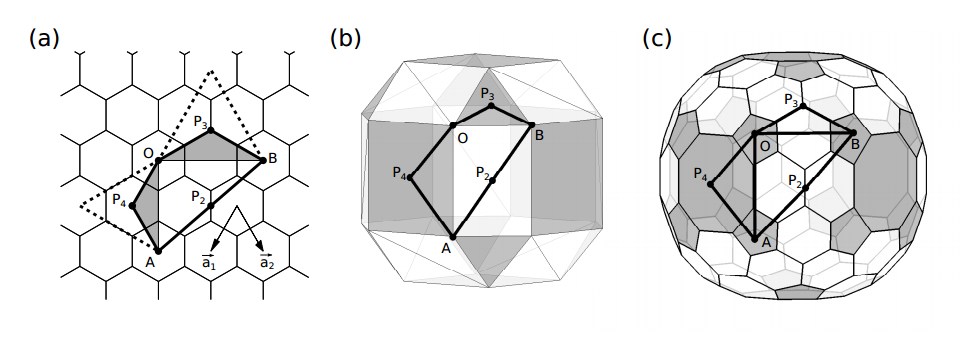
However, the climax of their paper comes when they finally discover a shape that has both octahedral symmetry and physically feasible bonds for a fullerene. The new molecule, in addition to the hexagons and pentagons associated with traditional fullerenes, also has four- and eight-carbon rings as well. Indeed, it turns out that there are four structural types of octahedral fullerenes.

The take-home message from Yuan-Jia and Bih-Yaw’ work is that the Brazuca ball does have a fullerene that is its molecular analogue, just like its predecessors at all the world cups dating back to 1970.

That will come as a great relief for topologists and football fans alike. Indeed, chemists might also be interested too. The next stage in this work will be for somebody with graphene and plenty of time on their hands to go out and actually make one of these molecules, perhaps in time for the 2018 World Cup in Russia.

Ref: arxiv.org/abs/1406.7058 : From the “Brazuca” ball to Octahedral Fullerenes: Their Construction and Classification

Follow the Physics arXiv Blog on Twitter at @arxivblog, on Facebook and by hitting the Follow button below

ORIGINAL: Medium

The Physics arXiv Blog on Jul 9